FPGA Applications in Photonics: Classical and Quantum Technologies
In today’s photonics and electro-optics landscape, systems require real-time precision, high bandwidth control, and deterministic behavior. Field Programmable Gate Arrays (FPGAs) are the ideal solution for these electro-optical applications
Introduction
Field-Programmable Gate Arrays (FPGAs) are reconfigurable integrated circuits that can be programmed to implement custom hardware logic. Unlike fixed-function ASICs or software running on CPUs/GPUs, FPGAs consist of an array of configurable logic blocks (e.g. lookup tables and flip-flops) with programmable interconnects, plus dedicated resources like DSP cores and memory blocks. This architecture enables massive parallelism and deterministic timing in signal processing[2]. In photonics – the science and technology of light – many applications demand precise timing (often sub-nanosecond jitter), high throughput data handling, and real-time processing that outpace general-purpose processors. FPGAs excel in these aspects by offering nanosecond-scale latency, hardware-level concurrency, and flexibility to interface with fast analog/digital converters and optical transceivers. This report explores the best uses of FPGAs in photonics, spanning classical electro-optic systems and emerging quantum technologies. We begin by explaining key FPGA attributes (architecture and jitter) and why they are beneficial for photonics. We then examine a range of photonics application areas – from high-speed optical communications and LIDAR to ultrafast lasers, spectroscopy, adaptive optics, and imaging – highlighting specific FPGA-based implementations from academia, laboratories, and industry. Finally, we review the role of FPGAs in quantum photonic systems, including quantum sensing, quantum communication (e.g. QKD), and quantum computing interfaces, with real-world examples of their use in photon counting and qubit control. Throughout, recent demonstrations (primarily from the last 5–7 years) are cited to illustrate state-of-the-art achievements.
FPGA Architecture, Timing Jitter, and Benefits for Photonics
FPGA Architecture: An FPGA is essentially a sea of logic gates that the user can wire together in nearly arbitrary ways. Modern FPGAs contain thousands of logic elements organized into configurable logic blocks (CLBs), each with lookup tables to implement boolean functions and flip-flops for storage, all connected via programmable routing fabric. They also include embedded memory (Block RAM), hardware multipliers/accumulators (DSP slices), and high-speed I/O transceivers. This architecture allows implementing custom digital circuits optimized for a specific task, and these circuits operate in true parallel fashion (every logic element can work concurrently on different bits of data) as opposed to sequential execution in CPUs [2]. For photonics, this means an FPGA can process multiple high-speed optical data streams or sensor signals simultaneously (e.g. multi-channel photodetectors or pixel arrays), and can perform pipelined computations on each clock cycle. Crucially, FPGA designs are synchronous – driven by a clock – which gives precise control over timing. Once configured, signal propagation through the FPGA’s logic occurs with fixed, known delays (on the order of nanoseconds), enabling deterministic response timing that is critical in feedback loops and timing-sensitive optical experiments.
Timing Jitter: Jitter refers to the small timing fluctuations or uncertainty in event occurrence times, often measured as the standard deviation of a signal’s timing error. In photonic systems, jitter in a clock or trigger can degrade performance – for example, timing jitter in a pulsed laser driver broadens the pulses, and jitter in detector gating or timestamping limits time-of-flight accuracy. FPGAs can help minimize and manage jitter in two ways. First, by bringing processing into hardware, they avoid the indeterminate latency of software and operating systems; an FPGA can respond to an input event within one clock cycle deterministically, whereas a microcontroller or PC might have unpredictable scheduling delays. Second, FPGAs can incorporate custom time-to-digital converters (TDCs) and phase-locked loops to measure and adjust timing with picosecond resolution. Modern FPGA-based time interval analyzers achieve digital time resolutions below 1 picosecond – for instance, one system reports a 780 fs timing resolution with an RMS jitter under 20 ps (liquidinstruments [7]). Such precise timing is extremely useful for photon counting and optical ranging applications. Additionally, multiple signals can be aligned or correlated in hardware with sub-nanosecond precision on an FPGA, which is very challenging via software. By using techniques like tapped delay lines in FPGA fabric, time intervals much shorter than the base clock period can be resolved, providing fine-grained control and measurement of optical pulse timing (liquidinstruments [7]). Overall, the low intrinsic jitter and deterministic timing of FPGAs make them ideal for synchronization tasks (e.g. locking laser pulses to detectors) and any photonic system where timing stability is paramount.
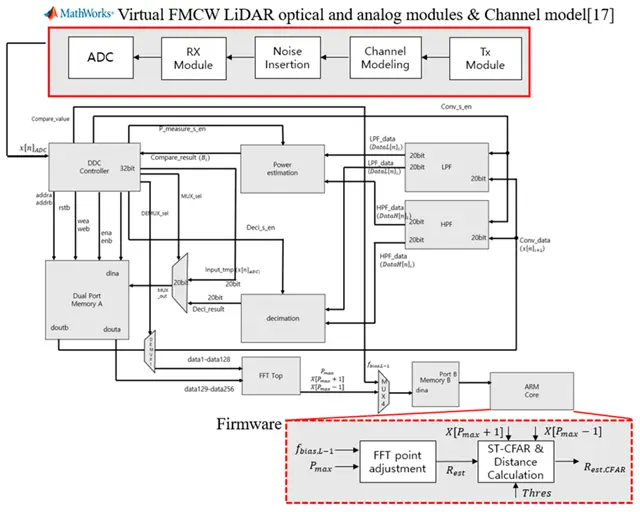
Example of an FPGA-based photonic system for LIDAR: Block diagram of an FMCW LIDAR processing architecture implemented on FPGA (bottom, “Firmware”), interfaced with the optical front-end modules (top red box, simulated in this case). The FPGA logic performs digital down-conversion (DDC), filtering (LPF/HPF), decimation, and FFT processing on the beat signal in real-time, and passes the reduced data to an embedded processor for distance calculation. Such an integrated, timing-critical system would be difficult to realize efficiently without the parallel, deterministic capabilities of an FPGA [3] mdpi.com.
Benefits in Photonics: The general advantages of FPGAs – reconfigurability, parallel processing, and low-latency control – map strongly to photonics needs. Many optical systems generate high data throughput (for example, gigabit-per-second serial data in optical communication, or megapixel cameras in imaging) which FPGAs can handle by distributing the workload across many logic elements or pipeline stages. Photonics experiments often must run in real-time, such as adaptive optics systems that correct a laser beam while it propagates, or a spectroscopy setup that adjusts in real-time to a changing signal. An FPGA can implement closed-loop controllers or signal processors that update every microsecond or faster, which is far beyond the capability of PC-based control. The hardware-level parallelism also allows complex algorithms (filtering, FFTs, neural networks, etc.) to be executed with deterministic throughput regardless of algorithmic complexity, so long as the design fits in the FPGA. This is critical in timing-sensitive applications: e.g., in a pulsed laser system, an FPGA can monitor each pulse and apply a correction or log an event with exactly the same delay each time, ensuring a stable timing relationship (minimal drift). In summary, using FPGAs in photonics yields: (1) Precise timing and low jitter for generating and measuring optical events, (2) High-speed signal processing close to the source (avoiding data bottlenecks of transferring to a PC), and (3) Reconfigurable logic that can be tailored to specific photonic experiments or standards, and updated as requirements evolve. These benefits have motivated widespread adoption of FPGAs in both classical optical systems and cutting-edge quantum photonic setups.
Demo Video: Real-Time Signal Acquisition and Analysis (NI CompactRIO FPGA System)
This demo video presents IZAK Scientific’s Acustics Emission System project, an advanced FPGA and real-time signal processing solution built upon the National Instruments CompactRIO (cRIO) FPGA platform. The system integrates multiple NI modules—including NI-9203 for current measurement, NI-9205 for voltage acquisition, and several high-speed NI-9223 modules for megahertz-range waveform sampling. It enables real-time parametric data acquisition across multiple channels, with sophisticated FPGA-based digital filtering, hit-detection, and data processing capabilities.
The FPGA efficiently manages high-throughput data streams, calculating key parameters such as Amplitude, Energy, Rise Time, Duration, and applying complex filtering algorithms directly in hardware. The processed data is then seamlessly transferred through dedicated DMA channels to a Real-Time (RT) layer, enabling precise waveform and parameter visualization, histogram analysis, and advanced scatter plot analysis via a user-friendly interface.
This solution exemplifies IZAK Scientific’s expertise in leveraging CompactRIO FPGA technology combined with LabVIEW Real-Time for demanding, precision-oriented photonic and electronic measurement applications.
High-Speed Optical Communication Systems
One of the most significant classical photonics application areas for FPGAs is high-speed optical communication. Fiber-optic communication links (and free-space optical links) often operate at tens of gigabits per second and require sophisticated digital signal processing (DSP) for modulation, demodulation, and error correction. FPGAs are frequently used as the digital engine in optical transceivers and research prototypes because they can keep up with the required data rates and implement custom algorithms. For example, in intensity-modulation direct-detection links using advanced modulation formats like PAM4 (4-level Pulse Amplitude Modulation), FPGA-based processors can pre-compensate and equalize nonlinearities in real-time. Hu et al. (2024) demonstrated a 24.576 Gbit/s short-reach optical link using an FPGA to implement a neural-network-based digital pre-distortion (DPD) algorithm [2]. In their system, a 14.7456 GBaud PAM4 optical signal (20 km fiber link) is processed by a 64-channel parallel multilayer perceptron on the FPGA, which pre-distorts the transmitter waveform to counteract fiber and device nonlinearities. This FPGA-based approach kept the bit error rate below the forward error correction threshold, achieving error-free communication at 24+ Gbps. The authors note that “Field-programmable gate arrays, with their real-time processing capability, high parallelism, and flexible programming features, are ideal hardware choices for meeting the demands of high-speed data transmission in optical communications.” [2]. Indeed, many optical communication experiments rely on FPGA boards for real-time DSP: tasks include carrier recovery and demodulation in coherent optical receivers, forward error correction coding/decoding, and framing at 100 Gbps and beyond. While commercial optical transceivers eventually use ASICs for these functions (to reduce cost per unit), FPGAs are indispensable in research and prototype stages due to their programmability and rapid development cycle – allowing testing of new modulation formats or DSP algorithms in working optical links.
Another niche in optical communications where FPGAs shine is free-space and underwater optical links, which often have unique modulation or synchronization schemes. For instance, researchers demonstrated an FPGA-based design for a 4 Gbps low-latency underwater optical communication system, showing that the FPGA could handle the tight timing for half-duplex transmission and quick turnaround between transmit/receive modes[2]. In Visible Light Communication (VLC) or optical wireless systems, FPGAs can perform real-time adaptation to changing channel conditions (like modulation adjustments based on ambient light), which would be too slow if done in software. In summary, FPGAs provide the muscle for high-throughput optical communication by executing custom, parallel DSP pipelines – from filtering and equalization to clock/data recovery – all with deterministic low latency. This makes them critical for achieving the requisite performance in systems such as coherent fiber links, short-range optical interconnects, and advanced optical modulation research.
LIDAR and Time-of-Flight Ranging
Light Detection and Ranging (LIDAR) systems send out laser pulses or chirped optical signals and measure reflections to determine distance or create 3D images of environments. FPGAs are widely used in LIDAR for both signal generation (timing the outgoing pulses or chirps) and signal processing (capturing return signals and computing distances) in real-time. A key challenge in LIDAR is timing accuracy – for a pulsed Time-of-Flight (ToF) LIDAR, measuring distances with centimeter accuracy requires timing optical pulse returns with on the order of 100 ps precision. FPGAs, with their low jitter and ability to implement high-resolution TDCs, are ideal for this. They can timestamp the departure and arrival of laser pulses and compute distances on the fly. Additionally, parallel processing is useful in LIDAR for handling multiple detection channels or multiple pulses in flight. Frequency-Modulated Continuous-Wave (FMCW) LIDAR is an advanced form that uses chirped (frequency-swept) lasers and measures distance via frequency shift of the beat signal. FMCW LIDAR offers high sensitivity and can measure velocity (via Doppler) but requires heavy signal processing (Fourier transforms to extract beat frequencies) at high data rates. FPGAs have been crucial in making FMCW LIDAR feasible by handling these computations in real-time. Kim et al. (2020) developed an FPGA-based FMCW LIDAR processing engine that significantly reduces hardware complexity while improving range resolution [3]. In their design, the analog optical front-end outputs a high-frequency beat signal (proportional to target distance); instead of performing a large 8192-point FFT in one go (which is hardware intensive), they use a digital down-conversion (DDC) technique in the FPGA to lower the sampling rate and then perform a 256-point FFT [3]. By doing so, they achieved distance measurements in 3 cm increments with an RMS error of about 3 cm, and further applied a constant false-alarm rate (CFAR) algorithm on the FPGA to improve the ranging precision to ~1.9 cm RMS. All signal processing – including mixers, decimation filters, power estimation, FFT, and peak detection – was implemented in the FPGA’s logic and Block RAM. Notably, the entire hardware module was verified on a Xilinx Zynq FPGA, and the approach could handle beat frequencies corresponding to distances up to 50 m at fine resolution [3]. This level of real-time performance would be extremely challenging without FPGAs; a CPU processing 8192-point FFTs at multi-megahertz rates would not keep up, whereas the FPGA can pipeline the operations.
Beyond FMCW, even in pulsed LIDAR systems for autonomous vehicles, FPGAs often provide the “brains”. They can generate the nanosecond-scale laser trigger pulses with consistent timing, and simultaneously start timing counters to measure the return. If multiple detectors are used (e.g. a SPAD array or multiple scanning angles), the FPGA can parallelize the time measurements on all channels. In some advanced multi-channel LIDAR prototypes, the FPGA not only measures times but also performs immediate calculations to create a depth map that can be streamed out. For example, a recent multi-channel chaos LIDAR system used an FPGA to coordinate the entire operation: it synchronized the pulsed laser source, controlled a MEMS beam-scanning mirror, and processed the chaotic return signals in real-time [11]. The result was a real-time 3D point cloud generation which would be unattainable without the tight integration of control and processing that the FPGA provided. Timing precision is also worth noting – FPGA-based TDC implementations for single-photon LIDAR can reach tens of picoseconds resolution. One FPGA LIDAR timing experiment achieved a synchronization jitter of ~150 fs RMS between pulse arrival times [11], highlighting that FPGAs can meet even the most extreme timing requirements in optical ranging.
In summary, FPGAs enable LIDAR systems to meet their two key demands: high-speed parallel processing of sensor data, and ultra-precise timing for distance measurement. This has been demonstrated in academic systems (improving FMCW LiDAR range resolution via real-time DDC/FFT on FPGAs and in industrial prototypes (self-driving car LIDAR units with on-board FPGA logic). As LIDAR moves toward higher resolution and faster update rates (for autonomous navigation or atmospheric monitoring), the role of FPGAs is only growing, often in hybrid FPGA-ASIC solutions or FPGA-SoC (system-on-chip) devices that combine FPGA fabric with embedded CPUs for additional processing.
Ultrafast Lasers and Spectroscopy
Ultrafast photonics involves lasers with picosecond or femtosecond pulses, frequency combs, and high-speed optical modulation – domains where timing is critical and data can be prodigious. FPGAs have found important uses in controlling ultrafast laser systems and in processing data from ultrafast optical measurements (such as spectroscopy). A prime example is dual-comb spectroscopy, an advanced spectroscopy technique using two frequency comb lasers. Dual-comb spectroscopy can achieve high-resolution broadband spectra without moving parts, but it requires phase-coherent averaging of data at high speed to attain good signal-to-noise ratio. Implementing this in real-time is challenging, and this is where FPGAs have made an impact. Chen et al. (2020) reported an FPGA-based real-time signal processor for dual-comb spectroscopy that performs computational coherent averaging on the fly[1]. By processing the free-running dual-comb interferograms in an FPGA, they achieved a 7× improvement in random noise compared to simply recording the raw data and averaging offline. In other words, the FPGA could align and average successive spectra in real-time, correcting for phase drifts between the combs, which led to a cleaner spectrum within the same acquisition time. This kind of real-time improvement is crucial for practical dual-comb systems and would be very difficult without an FPGA or similar hardware – the data rates from dual-comb interferometers (multiple MHz) are too high for PC processing in real-time, and the phase correction algorithms require deterministic, cycle-by-cycle operations well-suited to FPGA logic.
Another area is laser stabilization and pulse control. Ultrafast lasers often need active feedback to stabilize their repetition rate or carrier-envelope phase. FPGAs are used in some systems to lock the laser’s timing to an external reference (or vice versa) by processing detector signals (e.g., from a photodiode measuring pulses) and adjusting a cavity length actuator. The low latency of an FPGA control loop can correct timing errors every pulse (at tens of MHz repetition), something unattainable with a PC-based controller. Similarly, in pulse shaping and optical arbitrary waveform generation, FPGAs can be used to drive high-speed modulators with calculated waveforms in real-time, enabling dynamic control of ultrafast pulse trains.
In spectroscopy beyond dual-comb, many experiments require capturing transient optical signals at high speed. An FPGA can serve as a real-time spectrometer back-end: for example, in laser absorption spectroscopy, an FPGA might take a detector’s output (after ADC) and continuously compute absorbance or fit spectral lines at kilohertz rates for monitoring chemical processes. A recent work implemented a real-time laser absorption spectroscopy sensor on an edge computing platform (an embedded system with FPGA/SoC) to monitor gas concentrations at 10 kHz sample rate. By deploying a neural network on the FPGA/embedded device, they achieved an update rate of 62.5 Hz for gas measurements while handling the raw 10 kHz data stream internally. This shows how FPGAs enable on-line data reduction in spectroscopy, allowing sensitive measurements in harsh or remote environments without needing a bulky computer. The result was a compact, in situ sensor that could capture rapid changes in gas parameters (e.g. tracking combustion dynamics up to 200 Hz) entirely in real-time[12].
Overall, FPGAs enhance ultrafast laser and spectroscopy setups by providing real-time computational power and control. They can synchronize multiple optical channels, implement feedback loops for stabilization, and process measurement data at the high rates dictated by ultrafast phenomena. These capabilities are essential for experiments like pump-probe measurements, ultrafast microscopy, or spectroscopic monitoring of fast events, where huge volumes of data or rapid decisions (triggering, switching) are involved. By handling these in hardware, FPGAs allow scientists to observe and control ultrafast photonic events with a fidelity and speed that would otherwise be impossible.
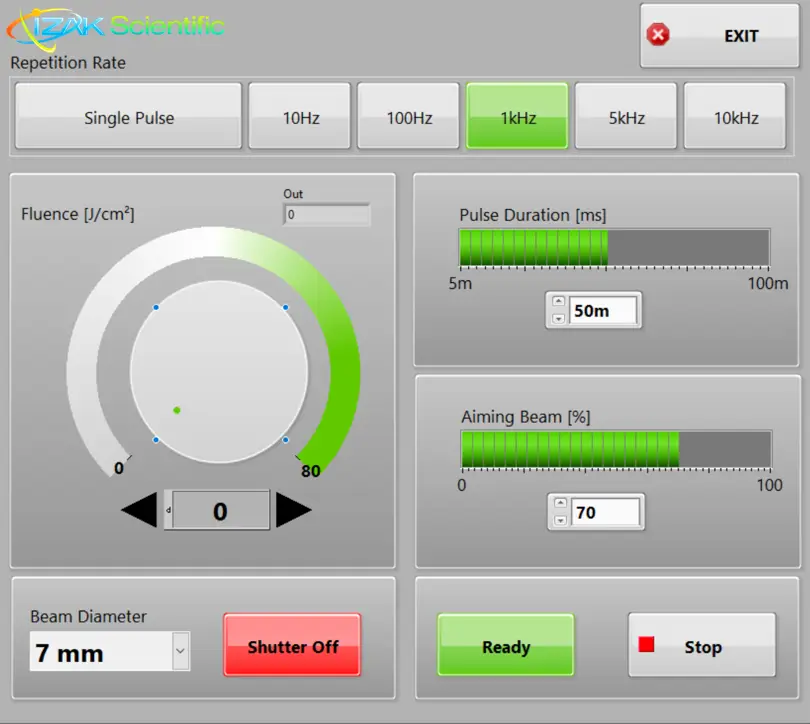
IZAK Scientific’s Laser Driver Control System implemented on an embedded National Instruments sbRIO FPGA platform. This system demonstrates precise real-time control over laser operations, tailored specifically for industrial and medical laser devices. It includes high-speed digital outputs for laser triggering and pulse shaping, analog outputs for dynamic intensity control, and PWM outputs for accurate aiming beam control. The sbRIO FPGA system provides deterministic, real-time control essential for synchronized and safe laser operation, capable of handling precise timing sequences with exceptional reliability. This solution highlights IZAK Scientific’s proficiency in delivering specialized FPGA-based hardware combined with custom LabVIEW applications for cutting-edge laser technology.
Adaptive Optics and Beam Control
Adaptive optics (AO) involves real-time adjustment of optical elements (like mirrors or lenses) to improve performance, commonly used to correct wavefront distortions. In astronomy, AO corrects atmospheric distortion using deformable mirrors driven by feedback from wavefront sensors. In high-power lasers and other photonics, AO can stabilize beams against thermal distortions or mechanical jitter. These systems typically require high-speed, deterministic control, since corrections must be applied quickly (often in sub-millisecond timescales) to be effective. FPGAs have become a key enabling technology for AO controllers thanks to their speed and parallel processing for sensor readout.
A concrete example is laser beam pointing stabilization. Zhang et al. (2023) designed a laser beam jitter control system using a fast steering mirror (FSM) and a camera, with an FPGA (NI FlexRIO) as the real-time controller [4]. In their setup, the CMOS camera detects the beam position, and the FPGA processes this in hardware to compute the error and send corrective commands to the FSM at high rate. By implementing the feedback loop in LabVIEW FPGA (a graphical FPGA programming environment) and optimizing for speed, they achieved a highly stabilized beam with very short response time. The closed-loop bandwidth was sufficient to correct platform vibrations and other disturbances, significantly reducing the beam deviation. The results showed improved stability and a fast transient response (short rise time) of the system, demonstrating the suitability of FPGA control for jitter reduction in engineering applications [4]. Without the FPGA, a general-purpose processor might only correct the beam at a few Hz or tens of Hz due to image processing latency, whereas the FPGA could handle the computations at kHz rates, aligning with the camera’s frame rate.
More generally in adaptive optics, an FPGA can acquire data from a wavefront sensor (e.g. an array of photodiodes or a Shack-Hartmann sensor), calculate the required actuator adjustments (using matrix-vector multiplication for wavefront reconstruction), and output commands to a deformable mirror – all within microseconds. For instance, AO systems for telescope or laser applications have been demonstrated with FPGAs running the control loop at 1–2 kHz update rates for dozens of actuators [10]. The deterministic nature of FPGA control is essential; every control cycle takes the same fixed time, ensuring stability of the control loop (no dropped or delayed cycles). In contrast, a PC-based AO control might jitter in its loop timing, introducing instabilities. FPGAs also allow parallel processing of multiple wavefront sensor channels (sub-apertures), which is crucial as the number of sensors/actuators grows in advanced AO (future giant telescopes will have thousands of sensors and actuators, where FPGAs or custom hardware are a must).
Another application is in ultra-intense laser facilities (which effectively borrow adaptive optics concepts from astronomy to stabilize high-power beams). A recent project implemented real-time wavefront stabilization for the Apollon petawatt laser using a high-speed controller to drive a deformable mirror and a Shack-Hartmann wavefront sensor. While in that case a GPU-based controller was used [10], the need for sub-millisecond latency was highlighted, and FPGA-based or hybrid FPGA solutions are being considered for even faster response. The general trend is that as the required control rate pushes into the tens of kHz (or as system complexity grows), FPGAs become the preferred platform for AO control.
In image processing and adaptive optics combined – for example, stabilizing an optical image or tracking an object – FPGAs can do real-time image analysis (such as centroid finding or correlation) on camera data and then actuate optics accordingly. The beam stabilization example above involved processing each video frame to find the laser spot position, essentially an image-processing task, done in hardware. The FPGA’s ability to handle the camera’s full frame rate with minimal latency made it possible to stabilize the beam in real-time. In more computational imaging contexts (like holographic imaging or phase retrieval), FPGAs have been used to accelerate the necessary FFTs and cross-correlations, enabling live reconstruction of images. Keywords associated with these FPGA-based optical systems often include “image processing” and “PID control,” underscoring that such FPGAs are effectively performing fast image-based control[4].
In summary, FPGAs empower adaptive optics and beam control by offering the speed, parallelism, and precise timing needed for feedback loops that involve many sensors and actuators. They have been successfully used to stabilize laser beams against jitter [4], to correct atmospheric distortion at kHz rates in telescopes, and to manage dynamic optical elements in applications like microscopy and free-space optics. The result is improved optical performance (sharper images, steadier beams) that would be unattainable without real-time FPGA-based control.
Photonic Image Processing and High-Speed Vision
Photonics isn’t only about analog optical signals – it also includes the processing of optical images and signals in the digital domain. “Photonic image processing” can refer to handling the data from optical imagers (cameras, lidar imagers, etc.) at very high frame rates or with optical pre-processing. FPGAs are widely used in high-speed vision systems and optical image processing where throughput and latency are critical. For instance, in a laser scanning microscope or an optical coherence tomography (OCT) system that produces megabytes of data per frame, an FPGA can perform real-time filtering, FFT, or image correction before storing or displaying the image. This is analogous to using a graphics processor, but the FPGA can be more deterministic and tailored to the exact algorithm.
One practical example is in smart cameras: cameras with built-in FPGAs can preprocess images (do compression, feature extraction, or thresholding) on-the-fly, reducing output data and enabling faster decision-making. In industrial inspection or optical tracking, an FPGA might analyze hundreds of frames per second, detecting events or computing guidance signals directly from the image stream. The benefit is that the immense parallelism of an FPGA can handle pixel-wise operations across an entire image concurrently. For example, if one needs to apply a filter or threshold to a million-pixel image at 1000 fps, that’s 1 billion pixel operations per second – a level at which a single CPU would struggle, but an FPGA with 1,000 parallel operations can manage by giving each pixel (or small group of pixels) its own processing pipeline.
In the context of the photonics applications listed, high-speed imaging often ties into other areas: LIDAR produces point clouds (images of distance), adaptive optics deals with wavefront sensor images, and quantum imaging (discussed later) may involve single-photon image reconstruction. FPGAs can thus serve as the bridge between the optical sensor and the digital outcome, implementing algorithms like centroiding (finding the center of a laser spot), frame accumulation, or even neural network inference on images in real-time. An example from research combined an FPGA with a single-pixel camera to do real-time computational imaging, where the FPGA would control a micromirror array to display patterns and simultaneously process the single-pixel detector readings to reconstruct an image on the fly – demonstrating a form of photonic image processing and adaptive control within the same FPGA system[4].
In summary, wherever images or optical spatial data need to be processed at high speed, FPGAs offer a solution. They can implement pixel-parallel pipelines that keep up with high frame rates, perform custom operations (which might be too unusual for a standard GPU to accelerate), and interface directly with camera sensors or spatial light modulators. The use of FPGAs in photonic image processing is evident in applications like real-time holography, high-speed tracking (e.g., tracking a laser pointer spot at thousands of frames per second), and any vision system where latency must be minimized (such as feedback based on images). By pre-processing and analyzing images in hardware, FPGAs enable faster and more efficient use of optical imaging data in both scientific instruments and industrial photonic systems.
Quantum Photonics and Quantum Technology Interfaces
Beyond classical photonics, FPGAs play a crucial role in quantum photonics and quantum technology interfaces. Quantum systems often involve delicate, fast events (like single-photon detections or qubit operations) that must be orchestrated or recorded with extreme timing precision and very low latency decisions. FPGAs, thanks to their deterministic and fast nature, form the backbone of many quantum experimental control systems.
Quantum Communication (QKD and Photon Counting)
Quantum Key Distribution (QKD) is a technology where secret keys are generated by sending quantum states (often single photons) between two parties. QKD protocols (like BB84 for discrete variables, or continuous-variable QKD) require not only the quantum optical transmissions, but also substantial classical post-processing: error correction, privacy amplification, and authentication, all of which must be done in real-time to generate a final key. These tasks can be computationally intensive, especially at high bit rates or when using high-dimensional encoding. FPGAs have been employed to accelerate QKD post-processing and to interface with high-speed optoelectronic components. For example, in continuous-variable QKD, an FPGA-based implementation of multidimensional reconciliation encoding was demonstrated by Lu et al. (2023) to handle error correction on a high-speed optical key stream [5]. By cleverly structuring the algorithm to fit FPGA architecture (using parallel operations and on-chip memory), they achieved a processing throughput up to 4.88 million symbols per second on a Xilinx Virtex-7 FPGA. This throughput enables real-time error correction even for high-rate CV-QKD systems, something that general CPUs would struggle with due to the combination of large block sizes and low latency requirements. The FPGA design processed 8-dimensional reconciliation coding, showing that such complex algebra can be done in hardware efficiently [5]. Similarly, other groups have used FPGAs for privacy amplification (hashing the corrected key down to a shorter secure key) – one recent implementation achieved handling of $>10^8$ bits in block size for privacy amplification using an FPGA cluster, vastly speeding up a step that could be a bottleneck in QKD [13].
At the hardware interface level, FPGAs often control the modulators and detectors in QKD. For discrete-variable QKD (like BB84 protocol), an FPGA can generate the pseudorandom bit sequence that drives an electro-optic modulator (to encode polarization or phase on each photon) and can timestamp detection events from single-photon detectors. The timing aspect is critical: single-photon avalanche diodes (SPADs) or superconducting nanowire detectors produce very narrow pulses when they detect a photon, and these must be timestamped with sub-nanosecond accuracy to sift the keys. FPGA-based time-taggers can record detection times with picosecond resolution, enabling accurate pairing of photon events with sent bits[7]. Moreover, an FPGA can apply gating to detectors (turning them on only when a photon is expected, to reduce noise) with precise timing. In an underwater QKD demonstration (2021) [14], an FPGA was used for the entire BB84 protocol logic in real-time, interfacing with the optics to generate polarized photons and measure results, showing that even a full QKD protocol can be embedded on a single FPGA device for field deployment. The result was stable secret key generation over a water channel, made possible by the self-contained FPGA system handling synchronization, basis sifting, error correction, and privacy amplification on-board.
Photon counting in a broader sense (not just for QKD) is also heavily FPGA-reliant. Quantum optics experiments often use single-photon counters (e.g. in quantum imaging, fluorescence lifetime measurements, or fundamental tests) and need to record the arrival times of photons at high rates. FPGA-based TDCs have achieved timing bins on the order of 10–20 ps [12], allowing researchers to build time-correlated single photon counting (TCSPC) setups without dedicated TDC chips. For instance, Liquid Instruments’ Moku:Pro device (FPGA-based) can timestamp photons with ~20 ps RMS jitter [7], which is sufficient for many quantum optics timing experiments. Additionally, FPGAs can implement real-time histograms or correlations of photon arrival times for experiments like Hanbury Brown–Twiss intensity correlations, providing immediate results rather than storing gigabytes of timestamps for later analysis [7].
In summary, FPGAs significantly enhance quantum communications by enabling real-time processing and precise handling of photonic qubits. They bridge the gap between the quantum physical layer (faint laser pulses or single photons) and the classical digital layer (error correction algorithms and key distillation). Without FPGAs or similar hardware, high-rate QKD systems would be limited by the latency and throughput of software processing, and the synchronization of single-photon events would be far less precise.
Quantum Sensing and Metrology
Quantum sensing exploits quantum states or phenomena to achieve ultra-sensitive measurements (for example, using entangled photons for improved imaging, or NV centers in diamond for magnetic field sensing). These experiments often involve coordinating lasers, detectors, and sometimes feedback based on quantum events. FPGAs are widely used in quantum sensing setups as the central controller and data acquisition system.
Take the example of an optical atomic clock or interferometric quantum sensor: One might have a pulsed laser interacting with atoms, and single-photon detectors reading out the state of the atoms. An FPGA can orchestrate the timing of laser pulses (down to ns precision), apply frequency or phase chirps via driving an acousto-optic modulator, and read the detector outputs to decide the next pulse sequence. Because these experiments sometimes need conditional logic (e.g. if an atom was detected in state A, apply sequence X next; if not, do Y), the reconfigurability of an FPGA is valuable – one can program such a decision tree into the hardware. FPGAs have been used, for instance, to implement real-time phase lock loops for stabilizing lasers to atomic transitions, or to do fast lock-in detection of signals in NV-diamond magnetometers (where the FPGA modulates a microwave drive and demodulates the fluorescence signal from the NV center in real-time). The extremely low jitter and fast computing means the FPGA can extract very weak signals buried in noise by coherent integration or filtering, effectively enhancing the sensor performance.
In quantum optics experiments, sometimes the experiment requires coincidence detection between photons – for example, heralded photon sources or entanglement experiments. FPGAs can monitor multiple detector channels simultaneously and identify coincident detections with nanosecond windows, then trigger some action or simply log the coincidences. Because all channels are within one FPGA, the relative timing can be calibrated tightly (down to picoseconds), which is much better than trying to combine separate devices. This is essential for observing quantum correlations or for quantum LiDAR schemes that look for simultaneous photon returns.
Another advanced capability is real-time feedback in quantum sensing. For example, in some cavity QED (quantum electrodynamics) experiments, an FPGA monitors photon counts leaking from a cavity and adjusts a magnetic field or laser intensity in real-time to keep the system in a desired quantum state (this is a form of active quantum stabilization). The feedback must happen faster than the system’s decoherence time, which can be microseconds – again, only an FPGA (or custom hardware) can operate on these timescales reliably.
In summary, FPGAs serve as the central classical node in many quantum sensing systems – they interface with quantum hardware (lasers, detectors, etc.), provide timing and control, and do initial processing of the sensor signals. This enhances the sensitivity and allows experiments that would otherwise require slow, offline analysis to be done in streaming mode. The result is more efficient data collection and even new measurement capabilities (like catching and reacting to quantum signals in flight). As quantum sensors move out of labs into field-deployable instruments, having an FPGA-based embedded controller is crucial for portability; indeed, many deployable quantum sensors (quantum gravimeters, portable atomic clocks, etc.) rely on FPGA/SoC devices for a compact, low-power control system that can run off batteries or mobile setups.
Quantum Computing Interfaces and Feed-forward Control
Quantum computing with photonics or other qubits involves delicate control of qubit states and often the need for feed-forward (adaptive) operations based on measurement outcomes. Whether the qubits are photons, trapped ions, or superconducting circuits, an FPGA-based control system is often used to interface between the classical digital domain and the quantum hardware. FPGAs can generate precisely shaped pulses (microwave, laser, or electro-optic) to manipulate qubits, and can read out signals (like a photodetector or a superconducting qubit readout) to determine the qubit state, all with minimal latency.
A salient example is the control of superconducting qubits, where commercial control systems (e.g. Quantum Machines’ OPX) are built around FPGAs. These systems allow users to program quantum pulse sequences with branching logic. For instance, QubiC 2.0 (an open-source qubit control system) uses an FPGA (on a Xilinx Zynq UltraScale+ RFSoC) to handle mid-circuit measurement and feed-forward for qubits [6]. The designers adopted a multi-core approach inside the FPGA, effectively giving each qubit its own processing core to ensure operations on different qubits can happen in parallel with precise timing. They store pulse shapes in the FPGA’s memory and can update pulse parameters (amplitude, phase, frequency) on the fly between pulses. With this setup, when a qubit is measured during a quantum circuit, the FPGA can decide in a few tens of nanoseconds how to adjust subsequent pulses (e.g. applying a correction if the qubit was in state 1 versus 0). This feed-forward latency is extremely low – on the order of the FPGA’s clock cycle (~10 ns or so) plus some pipeline delay – which enables protocols like quantum error correction where one must quickly respond to measurement outcomes. Indeed, with QubiC 2.0 they demonstrated conditional operations (feed-forward) and even synchronization of multiple FPGAs for scaling up [6].
In photonic quantum computing, active feed-forward is absolutely essential in some architectures (like linear optical quantum computing). For example, in certain photonic circuits, a measurement on one photon’s polarization will dictate how to switch a subsequent photon’s path or phase. This must happen while the latter photon is still in flight, often within nanoseconds for on-chip systems or microseconds for fiber delay line systems. FPGAs are the go-to solution for this: a photon detection is routed to an FPGA, which then toggles a Pockels cell or a fast optical switch to perform the next operation. A notable early demonstration used an FPGA to control a high-speed tunable beamsplitter for quantum computing with active feed-forward, achieving the required sub-microsecond switching based on measured photon events[15]. The FPGA logic was responsible for deciding the output of the tunable beamsplitter in real-time, something impossible to do with a PC. As a result, they realized a linear optics quantum gate with feed-forward, a stepping stone toward scalable optical quantum computing [15][16].
In summary, quantum computing interface electronics rely heavily on FPGAs to bridge the fast, parallel world of quantum hardware and the flexible world of classical control software. FPGAs provide ultra-low latency control, which enables mid-circuit adaptations (a key ingredient in advanced algorithms and error correction). They also ensure precise timing synchronization across multiple qubits or photonic channels – often, multiple DAC/ADC channels on an FPGA are all clock-synchronized to sub-ps skew, which is crucial for multiqubit gate calibration and interference of photons. Without FPGAs, quantum experiments would be forced to either operate in open-loop (no real-time decisions) or suffer long dead-times while waiting for a CPU to respond, both of which limit scalability. Therefore, FPGAs are a linchpin in quantum photonics and quantum computing, accelerating progress by unlocking experiments and protocols that demand fast, parallel, and adaptive control.
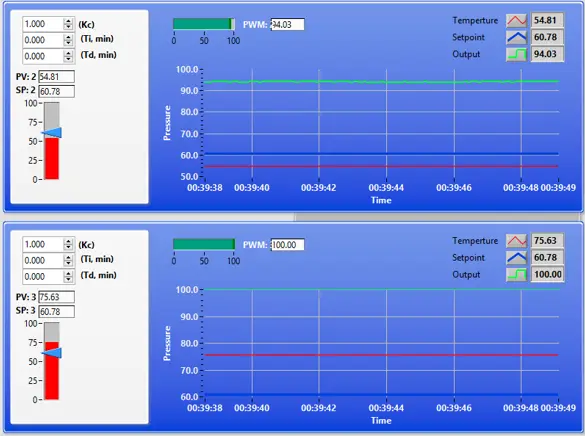
The second image presents IZAK Scientific’s sophisticated Laser Cooling and Thermal Management System, built upon the National Instruments sbRIO FPGA hardware. Designed to ensure optimal laser performance and longevity, this system implements advanced PID control loops for thermal regulation using multiple thermistor sensors strategically placed on both the cold and hot sides of a cooling device. The FPGA accurately processes temperature readings and controls PWM outputs to dynamically manage the thermal conditions, ensuring precise temperature stabilization even under demanding operational conditions.
Safety and reliability are integral features, with multiple digital inputs continuously monitoring critical temperature thresholds and promptly initiating protective responses. IZAK Scientific’s FPGA-based thermal management system thus guarantees stable, safe laser operations, demonstrating their capability in integrating sbRIO FPGA and LabVIEW Real-Time technologies for high-performance thermal control solutions.
Tzachi Sabati
CEO, IZAK Scientific
Physicist specializing in photonics and quantum technologies, with deep expertise in quantum sensors and advanced optical systems. Leads the Advanced Quantum Lab course at the Technion, bridging academic excellence with industry innovation. At IZAK Scientific, provides cutting-edge photonics-based solutions, developing customized inspection and sensing systems for R&D and production. Passionate about advancing quantum sensing applications and integrating novel technologies to meet industry needs.

