Introduction
Quantum entanglement is one of the most counterintuitive and fascinating phenomena in modern physics. First described by Einstein, Podolsky, and Rosen in 1935 as part of the famous EPR paradox, it challenges our classical understanding of locality and realism. Entanglement plays a critical role in quantum mechanics and serves as the foundation for numerous emerging technologies, including quantum computing, quantum communication, and quantum cryptography. As a cornerstone of the Second Quantum Revolution, entanglement is enabling unprecedented advancements in secure communications, ultra-precise sensors, and powerful computational paradigms.
From a Single Particle to Two-Particle Wave Function
Quantum mechanics describes the state of a single particle using a wave function \( \psi(x,t) \), which encapsulates all possible positions and momenta the particle can occupy. This wave function evolves according to the Schrödinger equation:
where \( \hat{H} \) is the Hamiltonian operator that dictates the system's energy dynamics.
When considering two particles, their joint wave function \( \Psi(x_1, x_2, t) \) now spans the combined degrees of freedom of both particles. If they are independent, their wave function factorizes:
However, when the particles are entangled, their wave function cannot be factorized into separate components. Instead, it must be expressed as a non-separable superposition:
This means the quantum states of both particles are intrinsically linked, leading to the phenomenon of quantum entanglement.
Theoretical Foundations of Quantum Entanglement
Quantum entanglement describes a scenario where two or more particles become so deeply correlated that their quantum states are interdependent, regardless of the distance between them. This interdependence is a direct consequence of quantum superposition and the linearity of quantum state evolution. The total quantum state of an entangled system cannot be described by the independent states of its individual components.
Mathematically, an entangled state can be represented as a superposition of two or more basis states. For a simple two-particle system, an entangled Bell state is expressed as:
or
where \( |00\rangle \) and \( |11\rangle \) indicate that both particles have the same state, while \( |01\rangle \) and \( |10\rangle \) correspond to opposite states. Measurement of one particle instantly determines the state of the other, seemingly violating classical notions of locality.
The peculiar nature of entanglement suggests that quantum mechanics does not adhere to classical determinism. This was a major point of contention in the EPR paradox, which questioned whether quantum mechanics was a complete theory. However, subsequent theoretical developments and experimental confirmations, particularly through Bell’s Theorem, have reinforced entanglement as a fundamental aspect of quantum mechanics rather than a mathematical anomaly.
Experimental Validation and Bell’s Theorem
John Bell formulated Bell’s Theorem in 1964 to test whether local hidden variable theories could explain quantum correlations. His inequality provided an experimentally verifiable criterion to distinguish between classical and quantum predictions. Since then, numerous experiments, including those by Alain Aspect in the 1980s and more recent loophole-free tests, have confirmed quantum entanglement’s nonlocal nature.
Below a recent experimental validation, carried out by Tzachi Sabati, involved correlation curve measurements of the entangled Bell state . The measurement was conducted by counting single photons as a function of polarization angles H, V, P, and M (from the Poincaré sphere) over a range of to . The resulting correlation curve provides direct evidence of quantum entanglement, as it demonstrates the violation of Bell’s inequalities. Unlike classical correlations, which adhere to local realism, the observed quantum correlations exceed classical bounds, confirming the intrinsic nonlocality of entangled states.
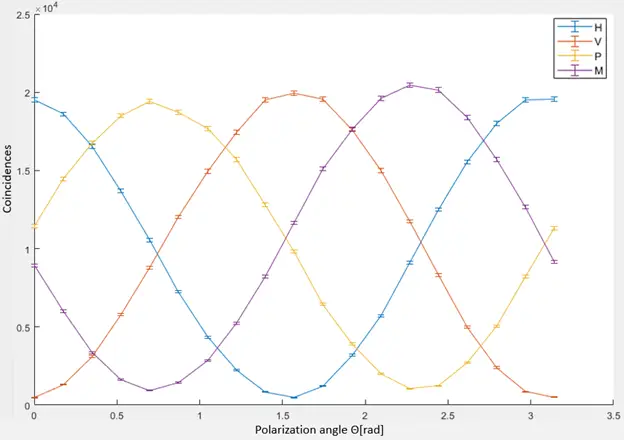
Experimental Correlation Curve Measurement of the Bell State, demonstrating quantum entanglement beyond classical limits.
Quantum Entanglement in Technology
Entanglement has led to groundbreaking applications in modern technology:
-
Quantum Computing: Quantum gates such as the CNOT gate leverage entanglement to enable operations that are exponentially faster than their classical counterparts. Algorithms like Shor’s factorization and Grover’s search algorithm exploit entanglement to perform tasks infeasible for classical computers.
-
Quantum Cryptography: Entanglement is the backbone of Quantum Key Distribution (QKD) protocols like BB84 and E91, ensuring unbreakable encryption through the fundamental principles of quantum mechanics.
-
Quantum Teleportation: Entanglement enables the transmission of quantum information between distant particles without physical movement, a crucial step toward future quantum networks.
-
Entangled Sensors: Quantum-enhanced sensors utilize entangled photons or atoms to achieve measurement precision beyond classical limits, useful in applications such as gravitational wave detection and medical imaging.
Challenges and Future Directions
Despite its potential, practical challenges remain in harnessing entanglement for real-world applications. Decoherence, noise, and environmental interactions disrupt entangled states, necessitating robust error correction and advanced isolation techniques. Researchers are exploring entanglement purification, quantum repeaters, and scalable quantum networks to overcome these limitations.
Conclusion
Quantum entanglement is not just a theoretical curiosity but a transformative force driving the Second Quantum Revolution. As technology advances, entanglement-based applications will redefine computation, security, and communication, shaping the future of quantum science and engineering. Understanding and harnessing entanglement will be key to unlocking the next generation of quantum technologies.
This post is part of a series exploring the Second Quantum Revolution. The next article will examine how entanglement is implemented in various quantum technologies and the critical components required for their realization. Come visit us at OASIS to discuss quantum sensing solutions tailored to your industry’s needs, where we will showcase all our activities in the field of photonics.
At IZAK Scientific, we specialize in custom quantum sensing solutions, helping industries leverage the precision and power of quantum technology. This article was written by a quantum researcher at the Technion, leading the advanced quantum lab course, reflecting deep expertise in the field.
References & Further Reading
-
J.S. Bell, On the Einstein Podolsky Rosen Paradox, Physics Physique Физика, 1964.
-
A. Aspect, Experimental Tests of Bell’s Inequalities, Nature, 1982.
-
R. Horodecki et al., Quantum Entanglement, Rev. Mod. Phys., 2009.
-
N. Gisin & R. Thew, Quantum Communication, Nature Photonics, 2007.
-
M. Nielsen & I. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2000.
Tzachi Sabati
CEO, IZAK Scientific
Physicist specializing in photonics and quantum technologies, with deep expertise in quantum sensors and advanced optical systems. Leads the Advanced Quantum Lab course at the Technion, bridging academic excellence with industry innovation. At IZAK Scientific, provides cutting-edge photonics-based solutions, developing customized inspection and sensing systems for R&D and production. Passionate about advancing quantum sensing applications and integrating novel technologies to meet industry needs.



































